La Fisica ha sempre trovato molto spazio nel mio insegnamento, non solo perché è una scienza contigua alla matematica, ma anche, e soprattutto, perché interpreta, in maniera assolutamente unica, il desiderio da parte dell’uomo di capire la realtà che lo circonda, di coglierne gli aspetti più nascosti, più difficili da comprendere e, proprio per questo, affascinanti.
Naturalmente quello che si può fare a livello di Scuola Media è seguirne le linee guida essenziali, ma ciò basta per intuirne la bellezza, per rimanerne coinvolti, sempre che il ragazzo sia sufficientemente attento, desideroso di capire, curioso al punto giusto, sollecitato ad esserlo.
Come si fa ad ottenere ciò? Non certo studiando la Fisica come se fosse un brano da ricordare, ma osservando il fenomeno, formulando delle ipotesi, verificando quella giusta e, in ultimo, traendo delle conclusioni che possono essere espresse da una legge, in sostanza procedendo con i tempi e le modalità del metodo sperimentale introdotto da Galileo Galilei.
Ecco l’essenza della Fisica, il metodo sperimentale, quello che, nel mio piccolo, ho sempre cercato di applicare: per me è impensabile insegnare Fisica semplicemente leggendo un libro.
E non è vero che è difficile realizzare ciò poiché le scuole non hanno adeguati laboratori, a volte basta un po’ di buona volontà e con poche cose, anche costruite da sé, si può fare Fisica.
I miei ragazzi ricorderanno il Prof. che camminava per i corridoi della scuola tenendo in mano un sacchetto di plastica contenete gli “strumenti” (cose prese qua e là, magari costruite con il legno), ad esempio un phon o un camioncino di plastica ( comprato in un negozio di giocattoli) e si presentava in classe o in laboratorio con esso.
Un collega una volta mi ha detto che un esperimento dimostrativo, fatto sulla cattedra, è una “magia”: posso anche essere, in parte,d’accordo, l’ideale sarebbe lavorare con i ragazzi a gruppi, sotto la guida dell’insegnante, ma quante scuole hanno il materiale sufficiente per poter realizzare ciò?
Ed allora basta una dimostrazione, con i ragazzi intorno alla cattedra, che osservano, traggono le conclusioni e poi vanno al loro posto a scrivere, sotto mia dettatura, tutta la procedura dell’esperimento, con relativo disegno, per renderli coscienti che un fenomeno, magari osservato da loro con superficialità o osservato per niente, esiste ed è possibile coglierne gli aspetti essenziali.
Alcuni esperimenti
Un argomento che mi ha sempre interessato e che ho proposto con strumenti quasi sempre costruiti da me o presi da qualche parte, è quello riguardante i moti della Terra.
Abbiamo iniziato la trattazione con le leggi di Keplero e considerando che un pianeta ruota intorno al Sole, secondo una traiettoria quasi circolare, in quanto obbligato dalla forza di gravità. A tale proposito abbiamo eseguito in aula il seguente esperimento: un bullone legato ad uno spago, un cartoncino abbastanza grande steso sulla cattedra, un foglio di carta copiativa sopra. Tenendo lo spago con la mano, abbiamo fatto ruotare il bullone sopra la carta in modo da lasciare sul cartoncino la traccia di una traiettoria circolare; ad un certo punto lo abbiamo lasciato: il bullone è andato a sbattere sulla parete laterale dell’aula.
Abbiamo osservato il cartoncino e su esso era ben evidente un tratto di linea tangente alla circonferenza, esattamente nel punto in cui il bullone, per inerzia, ha proseguito nel suo moto rettilineo.
Da questo semplice esperimento il concetto di forza centripeta, cioè la forza che costringe un corpo a muoversi secondo una traiettoria circolare, andando contro “il suo desiderio”, quello di proseguire in linea retta.
Per approfondire il concetto di forza centripeta abbiamo eseguito in aula l’esperimento classico del secchiello pieno d’acqua che viene fatto ruotare, secondo una traiettoria circolare, su un piano verticale, senza che l’acqua cada mai. A tale proposito abbiamo anche introdotto i concetti di sistema di riferimento inerziale e sistema di riferimento non inerziale.
Sistema di riferimento inerziale (un osservatore esterno)
Premessa:
Se un corpo è soggetto ad accelerazione, vuol dire che c’è una forza che ha prodotto tale accelerazione nella direzione della accelerazione stessa.
Consideriamo ora una generica particella che si muove lungo una circonferenza di raggio r con una velocità v costante in modulo ma non in direzione; in particolare chiamiamo V1 e V2 le velocità della particella in due istanti molto vicini.
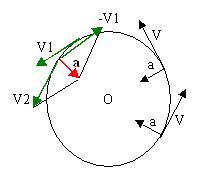
Facciamo ora la differenza tra i due vettori: V2 –V1
La stessa può anche essere scritta: V2 +(-V1), cioè facciamo la somma tra il vettore V2 e il vettore opposto a V1; tale differenza è rappresentata in figura e ottenuta mediante la regola del parallelogramma.
Indichiamo la differenza V2-V1 con Δv e l’intervallo di tempo tra i due istanti con Δt. Facciamo il loro rapporto:
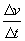
Quando i due istanti considerati sono molto vicini, cioè tende Δt a zero, il rapporto tende ad un valore limite uguale a 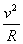 e il limite viene chiamato accelerazione istantanea. e il limite viene chiamato accelerazione istantanea.
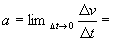 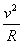
tale valore lo abbiamo ottenuto con una dimostrazione rigorosamente matematica che è possibile visualizzare in fondo alla pagina:
L’accelerazione, come si vede in figura, punta verso il centro della traiettoria e viene per questo chiamata accelerazione centripeta.
Essa è esattamente perpendicolare al vettore velocità, istante dopo istante.
Il suo modulo è sempre lo stesso mentre la direzione cambia continuamente.
Illustriamo l’esperimento del secchiello che ruota:
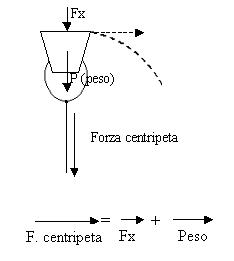
Quando il secchio pieno d’acqua viene fatto ruotare lungo una circonferenza verticale, i soggetti in azione sono due: il secchio stesso, che tenta, istante dopo istante, di andarsene per la tangente, ed una forza, esercitata dalla corda, che lo costringe a tale traiettoria e che, come abbiamo visto, produce una accelerazione diretta verso il centro.
Tale forza, chiamata forza centripeta, ha il seguente valore:
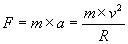
A questo punto la domanda:« Quando vale tale forza e qual è il valore minimo della velocità affinché, alla sommità, l’acqua non cada?».
Nel punto più alto della traiettoria la forza che trattiene il secchio non è solo quella esercitata dalla corda ma ha anche il contributo della forza peso. Le forze che agiscono sull’acqua sono pertanto due: la forza di gravità (peso) ed una forza Fx esercitata dalla corda attraverso il fondo del secchio; entrambe le forze costituiscono la forza centripeta, diretta verso il centro. Se si aumenta la velocità del secchio, alla corda sarà necessaria una forza maggiore per trattenerlo e quindi Fx dovrà aumentare; se si diminuisce la velocità Fx diminuirà. Il peso naturalmente non varia.
Il minimo valore della velocità si avrà quando Fx è uguale a zero, cioè quando, per un istante, basterà il solo peso a trattenere il secchio.
Dalla relazione 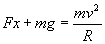 segue: segue:
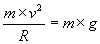
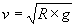
dove R è il raggio della traiettoria e g l’accelerazione di gravità.
Dalla descrizione si capisce che l’esperimento è stato analizzato secondo un riferimento inerziale, cioè quello di un osservatore esterno.
Ma se l’osservatore è solidale con il secchio, cioè si trova all’interno del secchio, com’è nel caso dell’acqua, il fenomeno può essere spiegato allo stesso modo o in maniera completamente diversa? In maniera completamente diversa.
Sistema di riferimento non inerziale (il secchio stesso)
Alla sommità la generica goccia d’acqua è sottoposta a due forze, la forza centrifuga, verso l’alto e il peso, verso il basso. Se, a causa di una velocità elevata, prevale la forza centrifuga, l’acqua viene schiacciata verso il fondo del secchiello, se, invece, a causa di una velocità minore, prevale il peso, l’acqua cade a terra. Se, a causa di una velocità adeguata, le due forze sono uguali in modulo, l’acqua non cade. È la stessa cosa che si ha all’interno di una navicella spaziale, in cui l’equilibrio tra la forza centrifuga e la forza di gravità ci fa vedere gli astronauti che svolazzano all’interno della stessa, come se non avessero peso, mentre la gravità è invece ben presente.
Per calcolare la velocità minima basta fare la seguente uguaglianza:
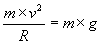
e ricavare la velocità.
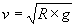
È la stessa formula che abbiamo ottenuto con il precedente ragionamento!
I moti della Terra
Una lampadina e un portalampada, un sostegno di legno, un mappamondo, un legnetto di circa due centimetri incollato sul mappamondo in corrispondenza dell’Italia, sono sufficienti per analizzare il moto di rotazione della Terra e l’inclinazione dei raggi del sole.
Attacchiamo, perpendicolarmente alla superficie del mappamondo, esattamente in corrispondenza dell’Italia, il legnetto che rappresenti un paletto posizionato verticalmente rispetto al suolo; di fronte al mappamondo, ad una distanza adatta, disponiamo la lampada a rappresentare il sole, la accendiamo. La parte della Terra illuminata rappresenta il dì, la parte in ombra rappresenta la notte. Ruotiamo il mappamondo in modo che il legnetto stia nella parte in ombra. Per il momento il Sole non è visibile. Immaginiamo di stare al posto del legnetto, guardando verso il polo Nord: appena incominciamo a ruotare il mappamondo in senso antiorario il Sole ci appare alla nostra destra, cioè ad est. Il Sole quindi sorge ad Est. Osserviamo ora l’ombra prodotta dal legnetto: è piuttosto lunga. Concludiamo che il Sole è basso all’orizzonte, è mattino.
Continuiamo a far ruotare il mappamondo: l’ombra prodotta dal legnetto diventa via via più corta, fino a quando, con il Sole perfettamente di fronte al legnetto, l’ombra assume la minima lunghezza ed è perfettamente allineata con il meridiano del luogo: è mezzogiorno.
La stessa ombra in inverno ha una certa lunghezza, in estate ha una lunghezza minore: trovandoci nella zona della Terra compresa tra i due tropici potremmo assistere a qualcosa a cui non siamo abituati, ombra zero. La perpendicolarità dei raggi del sole è presente infatti, a seconda della stagione, nella zona compresa tra il tropico del cancro (23° 27’ latitudine nord-21 giugno) e il tropico del capricorno (23° 27’ latitudine sud-21 dicembre).
Se poi continuiamo a ruotare ancora il mappamondo, l’ombra si allunga di nuovo, fino a quando il Sole scompare alla nostra vista: questa volta alla nostra sinistra, ad ovest.
Il sole sorge sempre ad est e tramonta ad ovest? Non è sempre così. Il sole sorge perfettamente ad est e tramonta perfettamente ad ovest solo in corrispondenza dei due equinozi, quello di primavera, il 21 marzo e quello di autunno, il 23 settembre. In inverno il sole sorge a sud-est e tramonta a sud-ovest mentre in estate il sole sorge a nord-est e tramonta a nord-ovest.
Il moto di rivoluzione
Con gli stessi strumenti si osservano le diverse stagioni: se il circolo di illuminazione, cioè la circonferenza che separa la zona della Terra illuminata da quella in ombra, taglia la stessa a metà, vuol dire che è il 21 marzo o il 23 settembre, il dì ha la stessa durata della notte ed i raggi del sole arrivano perpendicolari all’equatore.
Lo stesso circolo, che nel nostro emisfero (emisfero boreale), il 21 giugno, taglia la Terra in modo che la parte illuminata formi un arco avente la massima lunghezza rispetto alla parte in ombra, sta ad indicare che in quel giorno il dì ha la massima durata rispetto alla notte; la situazione è naturalmente opposta nell’emisfero australe. Si può anche osservare molto bene che la parte al di sopra del Circolo Polare Artico è sempre illumina: il Sole non tramonta mai.
Il moto della luna
Il moto della luna è pittosto complesso; la cosa importante da dire è che il piano della sua orbita è inclinato di circa 6° rispetto al piano di rivoluzione della Terra rispetto al Sole (eclittica). Tale inclinazione impedisce di avere una eclisse di luna e una eclisse di sole ad ogni passaggio del satellite dietro alla Terra e davanti alla Terra.
Ulteriori approfondimenti li rimando alla sezione: "Le risposte della Fisica"
Le immagini in sequenza delle fasi lunari hanno un'unica pretesa: farci comprendere meglio quello che, della luna, vediamo ogni giorno.
Con gli stessi strumenti e con in più una piccola palla appoggiata su un sostegno di legno, si possono evidenziare le fasi lunari. La palla illuminata, in modo da mostrare una piccola falce (la luna sorge al mattino, bassa all’orizzonte, ad est, più o meno nella stessa posizione in cui prima è apparso il Sole), 
poi, continuando nella rotazione della Terra, metà della luna (in effetti è un quarto),
la luna piena (metà della luna),  quando la stessa si trova dietro alla Terra, un po’ più in alto in modo da essere pienamente illuminata dal sole che si trova, sulla stessa linea, davanti alla Terra: noi, rivolti verso nord, cominciamo a vederla alla nostra destra, ad est, a sera, per tutta la notte e poi la vediamo tramontare alla nostra sinistra, ad ovest, al mattino. quando la stessa si trova dietro alla Terra, un po’ più in alto in modo da essere pienamente illuminata dal sole che si trova, sulla stessa linea, davanti alla Terra: noi, rivolti verso nord, cominciamo a vederla alla nostra destra, ad est, a sera, per tutta la notte e poi la vediamo tramontare alla nostra sinistra, ad ovest, al mattino.
ancora un quarto di luna, questa volta è però una luna calante

Misura della latitudine di Matelica
Con qualche classe di terza media abbiamo rilevato la latitudine della nostra città.
Come sappiamo, la latitudine di un punto P è l’angolo tra il punto stesso e l’equatore, misurato sul meridiano passante per P.
Tale misurazione deve essere effettuata nei giorni coincidenti con l’equinozio di autunno o di primavera, esattamente alle ore 12, in quanto nei due giorni indicati i raggi del sole sono perpendicolari all’equatore (praticamente paralleli lo sono sempre).
Alle ore 12 del 23 settembre ci siamo portati sullo spiazzo adiacente la scuola, abbiamo disposto perpendicolarmente al terreno un paletto e abbiamo misurato la lunghezza dell’ombra che lo stesso proiettava sul terreno. Il paletto e la sua ombra formano un triangolo rettangolo. Abbiamo annotato le due lunghezze.
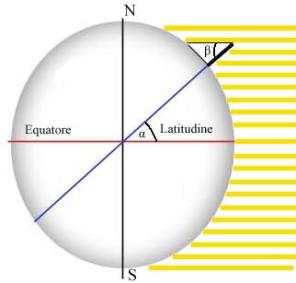
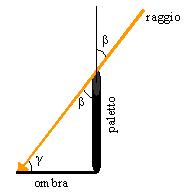
Se l’angolo α è la latitudine, anche l’angolo β, chiaramente uguale ad α, rappresenta la latitudine del luogo.
A questo punto, con i dati in nostro possesso, abbiamo costruito un triangolo in scala ridotta e misurato con un goniometro l’angolo β, la latitudine di Matelica. La latitudine di Matelica è 43° 15’ 21’’(dato preso da Internet).
Per un ragazzo delle superiori non è necessario fare la riduzione in scala e quindi adoperare il goniometro in quanto, una volta misurata la lunghezza dell’ombra e conoscendo la lunghezza del paletto, l’ampiezza dell’angolo β, e quindi la latitudine, può essere determinata dalla seguente relazione:
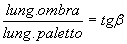
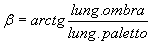
se:
lunghezza paletto = 1 m
lunghezza ombra = 0,94 m
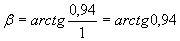
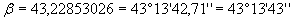
Alcuni dati astronomici di Matelica
Una volta nota la latitudine e conoscendo il raggio terrestre, è possibile, ad esempio, calcolare la circonferenza del parallelo passante per Matelica:
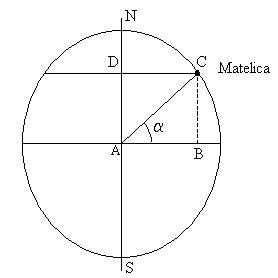
AC = raggio terrestre = 6370 km
AB = DC = raggio del parallelo passante per Matelica
Latitudine di Matelica = 43°15’21’’
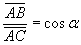
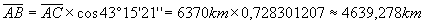
raggio del parallelo passante per Matelica = 4639,278 km
circonferenza del parallelo = 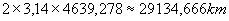
ancora:
conoscendo la lunghezza della circonferenza, possiamo calcolare il valore della velocità periferica cui gli abitanti di Matelica sono soggetti:
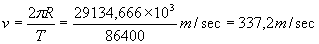
che equivalgono a 1213,92 km/h
In Italia la velocità periferica varia dai 1334 chilometri orari di Siracusa (latitudine 37 gradi) ai 1167 di Bolzano.
(all’equatore la velocità periferica è 463 m/sec = 1666,8 km/h)
naturalmente la velocità periferica è massima all'equatore in quanto i suoi punti sono i più distanti dall'asse, mentre è zero in corrispondeza dei due poli.
ancora:
conoscendo la velocità e il raggio, possiamo calcolare la forza centrifuga che gli stessi abitanti subiscono:
facciamo l’esempio di una persona di massa 80 kg (784 Newton di peso)
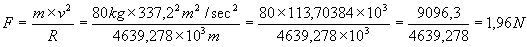
(all’equatore la forza centrifuga, a parità di massa, è di 2,7 N)
A questo punto è però necessario fare una precisazione:
la forza centrifuga, essendo direttamente proporzionale alla velocità periferica, è massima all'equatore e poi, man mano che ci si avvicina ai poli, diminuisce, fino ad annullarsi completamente.
Inoltre
la Terra è schiacciata ai poli, per cui la forza di attrazione dovuta alla sua massa, essendo inversamente proporzionale alla distanza dal centro, aumenta, sempre man mano che si va verso i poli.
I due effetti, quello della forza centrifuga e quello della forza di attrazione, combinati insieme, producono una gravità e quindi una accelerazione g che è minima all'equatore e massima ai poli.
All'equatore: g = 9,7803
Ai poli: g = 9,8321
conseguenza: un corpo, a parità di massa, ha peso
minimo all'equatore e massimo ai poli.
la combinazione dei due effetti è mostrata in figura:
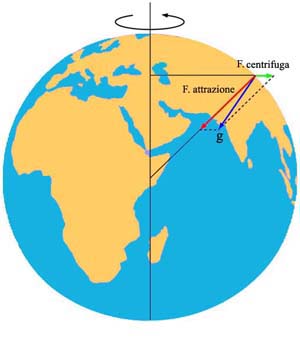
La forza centrifuga è responsabile dello schiacciamento della Terra ai poli:
utilizzando un semplice strumento che avevo in casa (di mia madre), abbiamo potuto verificarlo insieme ai ragazzi:

--------------------------------------------------------------------------------------------------------------------
Dimostrazione matematica del valore della accelerazione centripeta
Importante: le grandezze vettoriali sono rappresentate in grassetto
Come sappiamo, un vettore può essere scomposto nella somma dei suoi due vettori componenti:
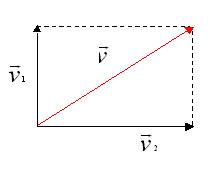
 = = 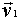 + + 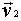
In un sistema di assi cartesiani un vettore può essere scomposto nelle sue componenti ax ed ay
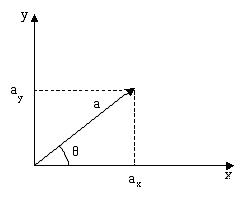
se si conoscono ax e ay (coordinate cartesiane), il valore dell’ampiezza di a si ottiene secondo la seguente relazione:
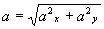
se invece si conoscono a e l’angolo θ (coordinate polari), le sue componenti si ottengono mediante le seguenti relazioni:
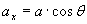
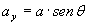
A volte un vettore può essere scritto come prodotto di un vettore unitario (versore), nella direzione di a, e il suo valore scalare:
a = 4
fissato il vettore unitario u 
a = u×a = 4 u
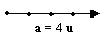 
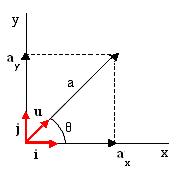
Rappresentiamo ora un vettore sul piano cartesiano, avente una inclinazione di 45° rispetto all’asse delle ascisse e indichiamo con i il versore dell’asse x e con j il versore dell’asse y. È importante notare che i versori i e j non necessariamente devono essere spiccati dall’origine degli assi; come tutti i vettori, essi possono essere traslati a piacere nello spazio delle coordinate purché le loro direzioni rispetto agli assi coordinati si mantengano inalterate.
L’ampiezza di a è 4
Fissiamo ad 1 l’ampiezza del versore ua di a e dei versori i e j

a = ua × a = 4 ua
ax = 4 × cos 45° i = 2,8284 i
ay = 4 × sen 45 j = 2,8284 j
Il vettore a può allora essere così scritto:
a = 2,8284 i + 2,8284 j
l’ampiezza di a si trova applicando il teorema di Pitagora:
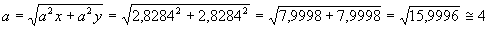 
Conclusione: l’ampiezza di a è 4 (è quanto sapevamo dall’inizio);
un vettore può essere espresso in funzione delle sue componenti e dei versori dell’asse x e dell’asse y
La rappresentazione è la seguente:
Facciamo ora un esempio di come, dati due vettori, possiamo effettuare la loro somma e la loro differenza rappresentandoli sul piano cartesiano:
Dati i due vettori, a e b, determinare analiticamente il vettore somma e il vettore differenza.
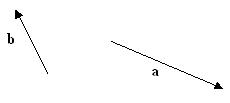
Trasliamo i due vettori in un sistema di assi ortogonali
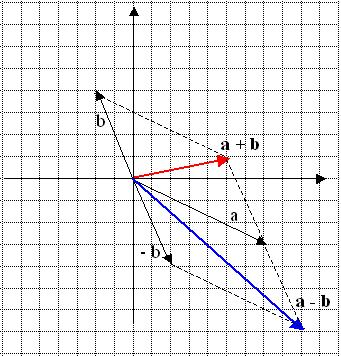
I due vettori possono essere così scritti:
a = 7i - 3 j
b = -2i + 4 j
la loro somma sarà:
a + b = (7i - 3 j) + (-2i + 4 j) = 7i - 3 j – 2i + 4 j = 5i + 1j
la loro differenza sarà:
a – b = (7i - 3 j) - (-2i + 4 j) = 7i - 3 j + 2i - 4 j = 9i – 7j
Lo si può verificare facilmente osservando la rappresentazione cartesiana
Vogliamo ora effettuare un procedimento puramente matematico per determinare il valore della accelerazione centripeta di un punto materiale che si muove su di una traiettoria circolare. La velocità è costante in modulo ma non in direzione.
La circonferenza è inserita in un sistema di assi cartesiani; i vettori della velocità sono considerati in due istanti diversi t1 e t2. Vogliamo determinare il valore della accelerazione istantanea nel punto P.
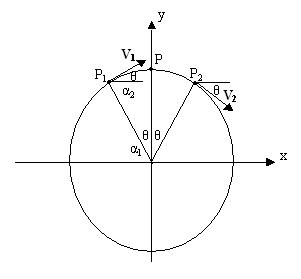
Come si può verificare dalla figura il vettore V1 forma con l’asse delle x lo stesso angolo che il raggio forma con l’asse delle y in quanto entrambi differenza di un angolo di 90° con un angolo α1 e con un angolo α2 uguali (alterni interni di due rette parallele tagliate da una trasversale).
La stessa cosa si può verificare per il vettore V2 rispetto allo stesso angolo.
Indicando con V il valore scalare della velocità, con i e j i versori rispettivamente dell’asse delle x e dell’asse delle y e immaginando una traslazione degli assi nel punto P1 e poi nel punto P2, possiamo scrivere:
V1 = (V· cos θ)i + (V· sin θ)j
V2 = (V· cos θ)i + (-V· sin θ)j
Facciamo la differenza V2 – V1
V2 – V1 = V· cos θ i - V· sin θj - V· cos θi -V· sin θj = -2 V· sin θj
Consideriamo ora la formula della accelerazione media che il punto materiale subisce nel passaggio dal punto P1 al punto P2:
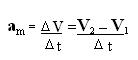
poiché V2 – V1 = -2 V sen θj
possiamo scrivere: am = 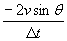 j j
vediamo che l’accelerazione media punta nel verso negativo dell’asse delle y.
Per avere una conferma visualizziamo la seguente immagine e calcoliamo il valore della differenza tra le due velocità:
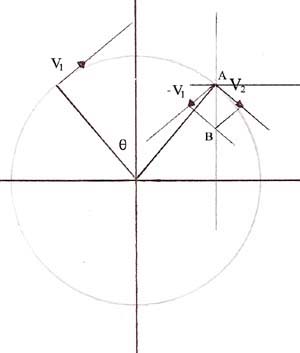
L’angolo θ ha ampiezza 40° e i due vettori velocità misurano sul foglio 1 cm.
Applicando allora la seguente relazione: V2 – V1 = -2×V×sen 40°, si ottiene:
V2 – V1 (segmento AB)= -2×1×0,64278 = 1,2855
Il valore è esattamente quello che si rileva effettuando la misurazione sul foglio in cui è stato disegnato il grafico. Si può verificare ancora che
il vettore differenza ha il verso negativo dell'asse delle y.
A noi interessa però l’accelerazione istantanea nel punto P. Per completare il calcolo abbiamo bisogno di  t, cioè il tempo necessario al punto materiale per andare da P1 a P2. t, cioè il tempo necessario al punto materiale per andare da P1 a P2.
Esprimiamo l’angolo al centro non in gradi ma in radianti
Premessa: si definisce radiante l’angolo al centro di una circonferenza, di raggio arbitrario, che sottende un arco avente la stessa lunghezza del raggio
Da ciò deriva che se l'angolo al centro ha come unità di misura il radiante e l'arco il raggio, le loro misure sono espresse dallo stesso numero:
lunghezza dell’arco = lunghezza raggio = 1r
angolo al centro = 1 radiante
lunghezza dell’arco = 2πr (angolo giro)
angolo al centro = 2π radianti (intera circonferenza)
angolo al centro = 2θ radianti
lunghezza dell’arco = 2θr
La lunghezza dell’arco è lo spazio che il punto materiale deve percorrere per andare da P1 a P2.
Dalla formula della velocità ricaviamo:
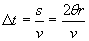
l’accelerazione media allora diventa:
am=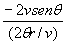 j = j =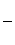 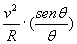 j j
a noi interessa l’accelerazione nel punto P. Per calcolare tale valore dobbiamo fare in modo che i punti P1 e P2 si avvicinino a P; ciò avviene quando l’angolo θ tende a zero.
Dalla formula precedente sappiamo che si può matematicamente dimostrare che il rapporto 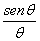 tende ad 1 al tendere di θ a zero tende ad 1 al tendere di θ a zero
quindi l’accelerazione nel punto P diventa: a =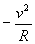 j j
l’accelerazione è diretta verso il centro della circonferenza, secondo la direzione indicata dall’asse delle y e il suo modulo è: 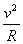
è una accelerazione istantanea che quindi, istante dopo istante, punta esattamente verso il centro della circonferenza, in maniera radiale rispetto al vettore della velocità. Tale accelerazione la chiamiamo accelerazione centripeta.
|

